Radiation belt electrons are distributed in two distinct zones: the inner zone that is relatively stable and the outer zone that is very dynamic. The flux of energetic electrons in the Earth’s outer radiation belt can vary by several orders of magnitude over time scales less than a day in response to changes in properties of the solar wind instigated by solar activity. Variability in the radiation belts is due to an imbalance between the dominant source and loss processes that are caused by a violation of one or more of the adiabatic invariants. For radiation belt electrons, non-adiabatic behavior is primarily associated with energy and momentum transfer during interactions with various magnetospheric waves [Thorne, 2010]. The most dramatic variations in the outer belt occur during magnetic storms, when the enhancement in the ring current causes a global decrease in the ambient magnetic field [e.g., Tsyganenko, 1996]. Reduced magnetic field affects the adiabatic drifts of radiation belt particles and causes an outward motion of radiation belt electrons with an accompanying loss of energy, which in turn causes an adiabatic decrease in radiation belt flux [e.g., Kim and Chan, 1997] in addition to loss by scattering into the atmosphere [Millan and Thorne, 2010] and transport to the magnetopause [Ukhorskiy, 2006]. To differentiate between adiabatic and non-adiabatic changes in the radiation belts a simultaneous study of the radiation belts and ring current dynamics is needed [Jordanova, 2012].
There are three adiabatic invariants [Roederer, 1970] associated with the three basic periodic motions: gyro-motion, the bounce motion in the Earth's magnetic mirror field, and the azimuthal drift due to magnetic gradients. Each invariant can be violated when the system is subject to fluctuations on time-scales comparable to or shorter than the associated periodic motion [Schulz and Lanzerotti, 1974]. ULF waves, with periods comparable to tens of minutes, cause a violation of the third invariant, resulting in radial diffusion. Since the power in ULF waves is considerably enhanced during magnetic storms [Mathie and Mann, 2000], radial diffusion is a potentially important mechanism for energetic electron acceleration [Rostoker et al, 1998; Elkington et al., 1999; Hudson et al., 2001; O'Brien et al., 2001; Shprits and Thorne, 2004] or loss [Shprits et al., 2006; Jordanova et al., 2008] during storm conditions, dependent on the radial gradient in phase space density. Higher frequency ELF and VLF waves cause violation of the first two invariants and lead to pitch-angle scattering loss to the atmosphere [Thorne and Kennel, 1971; Lyons et al., 1972; Abel and Thorne, 1998a,b] or local stochastic energy diffusion [Horne and Thorne, 1998; Summers et al., 1998; Horne et al., 2005; Miyoshi et al., 2003].
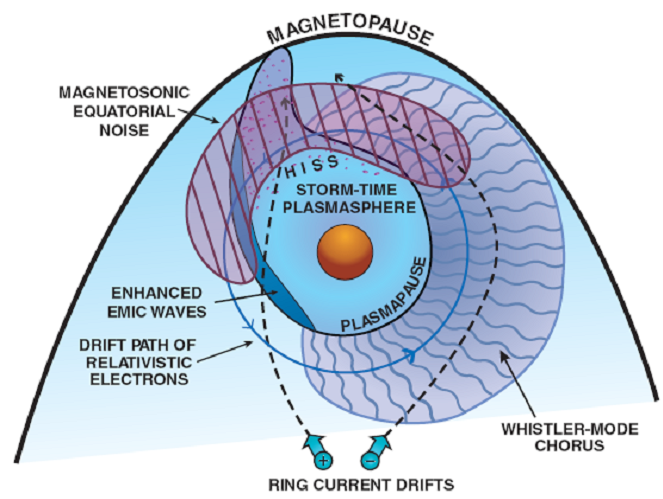
During storm conditions, the power spectral density of ELF and VLF waves is also strongly enhanced [Meredith et al., 2003; Li et al., 2009a]. Consequently, during disturbed conditions, all three adiabatic invariants can be violated simultaneously, and multi-dimensional diffusion models [Jordanova and Miyoshi, 2005; Jordanova et al., 2008; Fok et al., 2008; Tao et al., 2008, 2009; Varotsou et al., 2008; Albert et al., 2009; Shprits et al, 2009; Subbotin and Shprits, 2009; Tu et al., 2009] are required to differentiate between the different source and loss processes. Such codes require accurate specification of the rate of radial diffusion DLL, pitch-angle scattering Daa, and energy (or momentum) diffusion DEE. Each diffusion coefficient requires a global specification of the power spectral intensity of all relevant plasma waves. A schematic model for the regions where some of these waves are excited is given in Figure 1. The excited waves cause particle scattering, which modifies the particle pitch-angle distribution and leads to loss in the atmosphere. During resonant scattering, energy can also be transferred from the low-energy population (which provides the source of the waves) to the high-energy tail population, causing in situ local acceleration [Horne and Thorne, 2003]. The variability of such scattering during geomagnetically active periods requires precise measurement of the intensity of all important magnetospheric waves. Accurate measurement of the large-scale magnetic fields is needed to determine the evolution of ring current as well as the source population and/or the adiabatic effects on energetic electrons.
Figure 1. A schematic diagram of the equatorial magnetosphere illustrating the spatial regions for wave-particle interactions between relativistic electrons and important plasma waves. Whistler-mode chorus can induce micro-burst precipitation (Thorne et al., 2005) and local stochastic acceleration (Summers et al., 1998; Horne et al., 2005) along a broad portion of the electron drift path between midnight and noon. Equatorial magnetosonic waves contribute to local electron acceleration. Strong pitch-angle scattering by EMIC waves along the duskside plasmapause can cause intense but localized precipitation in the dusk sector (Jordanova et al., 2008). Electrons are also subject to weak diffusion scattering on the dayside during resonance with plasmaspheric hiss. Relativistic electron drift times are typically less than 10 minutes and the average rate of precipitation loss or stochastic acceleration must be averaged over both the bounce and drift motions in this highly variable environment. |
The magnetospheric waves responsible for radiation belt dynamics have recently been reviewed by Thorne [2010]. A brief summary of our current understanding of these waves is given below.
Ultra Low Frequency Waves (mHz) are excited at the magnetopause boundary in response to velocity shear [Claudepierre et al., 2008] or solar wind pressure fluctuations [Ukhorskiy et al., 2006; Claudepierre et al., 2009]. Hydromagnetic waves may also be excited internally by natural instability of the magnetospheric plasma. These ULF waves cause radial diffusion transport and associated energy change in the trapped particle population. The rate of radial transport is dependent on the power spectral intensity of the waves and tends to be much faster in the outer magnetosphere.
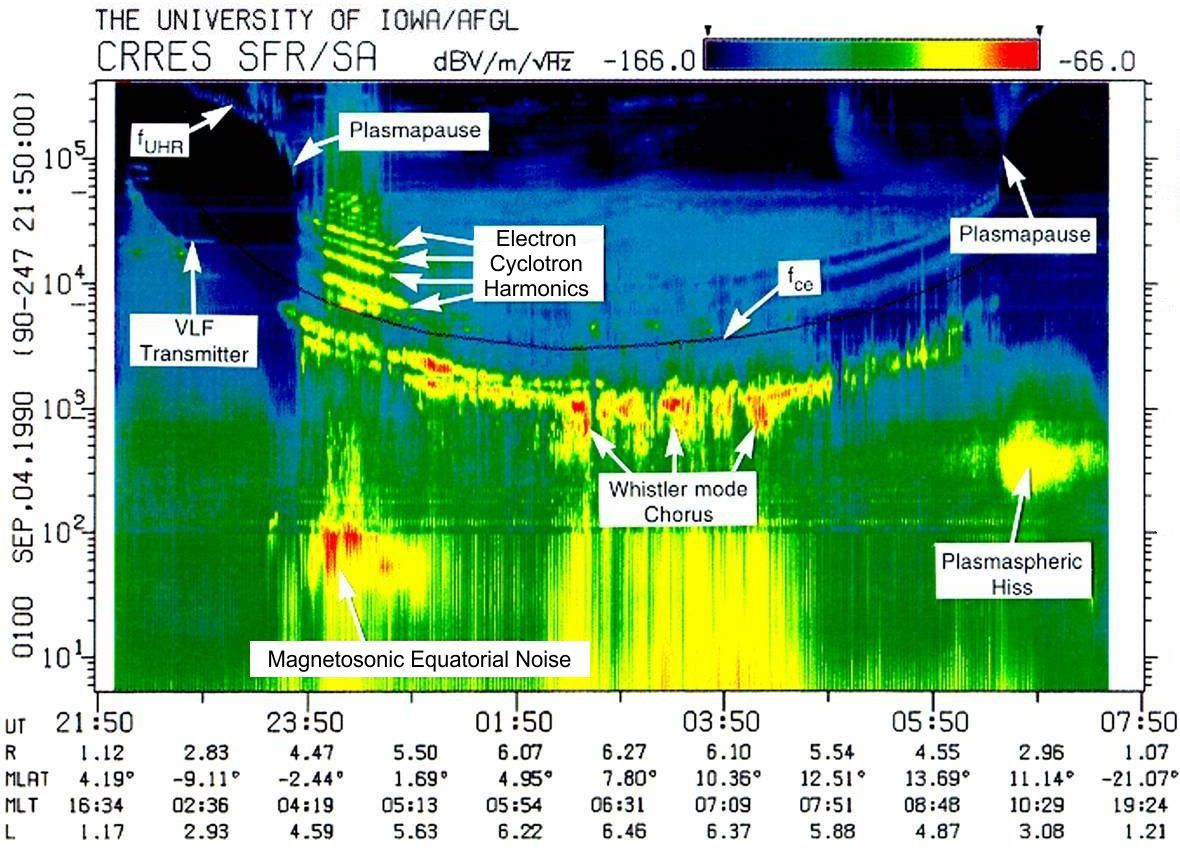
Chorus Emissions are discrete coherent whistler mode waves, which occur in two distinct bands above and below one-half the electron gyrofrequency fce as shown in Figure 2 [Tsurutani and Smith, 1974]. Chorus is important because it plays a dual role in both the loss and local acceleration of radiation belt electrons [Bortnik and Thorne, 2007] and is the dominant scattering process leading to diffuse auroral precipitation [Ni et al., 2008; Nishimura et al., 2010; Thorne et al., 2010]. Recent statistical analyses of the global distribution of chorus observed on the THEMIS spacecraft indicates that the spectral intensity is highly variable and responds to geomagnetic activity [Li et al., 2009a]. Chorus is enhanced over a broad spatial region [Hayosh et al., 2010] exterior to the plasmapause (see Figure 1) associated with cyclotron resonant excitation during the convective injection of plasma sheet electrons into the magnetosphere [Li et al., 2008, 2009b; Jordanova et al., 2010a]. Nightside chorus is strongest inside L=8, and is also confined to latitudes below 150, due to strong Landau damping of oblique waves during their propagation towards higher latitude from the equatorial source region [Bortnik et al., 2007]. In contrast, dayside chorus is found over a broad range of latitudes, is most intense in the outer (L~8) magnetosphere, and shows less dependence on geomagnetic activity [Tsurutani and Smith, 1977; Li et al., 2009a]. The wave normal distribution of chorus is required to accurately evaluate resonant electron energies and quantify the associated rates of scattering [Shprits and Ni, 2009]. Unfortunately, recent satellite observations [Chum et al., 2007;Breneman et al., 2009; Santolik et al., 2009; Haque et al., 2010] indicate a wide range of values for this key property, which adds uncertainty to modeling studies.
Equatorial Magnetosonic Waves are highly oblique whistler-mode emissions excited within a few degrees of the equatorial plane at frequencies between the proton gyrofrequency and the lower hybrid [e.g., Santolik et al., 2004]. The waves are observed both inside and outside the plasmapause and are excited by a cyclotron resonant instability with a ring distribution of injected ring current ions [Horne et al., 2000; Meredith et al., 2008; Chen et al, 2010b]. MS waves also undergo a Landau resonance with radiation belt (100 keV – few MeV) electrons, and the spectral properties of intense MS waves observed on Cluster have been used to demonstrate that the timescale for energy diffusion (~day) can be comparable to that due to chorus scattering [Horne et al., 2007]. Test particle scattering of electrons in a finite amplitude MS wave have confirmed the rate of Landau resonant scattering [Bortnik and Thorne, 2010] and demonstrated additional non-resonant “transit time” scattering due to the equatorial confinement of MS wave power.
Plasmaspheric Hiss is an incoherent whistler-mode emission mostly confined within the dense plasmasphere and within dayside plasmaspheric plumes, which is mainly responsible for the formation of the quiet time electron slot between the inner and outer radiation belt [Lyons and Thorne, 1973; Abel and Thorne, 1998]. Recent ray trace modeling has shown that hiss originates from a subset of chorus emissions that avoid Landau damping during propagation from the equatorial source region to higher latitude. Such waves also propagate to lower L where they enter and are trapped within the plasmasphere, where the discrete chorus emissions merge together to form incoherent hiss [Bortnik et al., 2008b, 2009a]. The unexpected association between hiss and chorus has been confirmed by simultaneous observations on two THEMIS spacecraft [Bortnik et al, 2009b] and differences in the statistical MLT distribution of the two emissions has been explained by 3D ray tracing [Chen et al., 2009b].
Figure 2. Spectrogram of waves observed on CRRES, showing various magnetospheric waves which resonate with energetic electrons.
|
Electromagnetic Ion Cyclotron Waves are discrete electromagnetic emissions, which occur in distinct frequency bands separated by multiple ion gyrofrequencies. The EMIC source region is typically confined within ~ 10 degrees of the geomagnetic equatorial plane, and the Poynting flux at higher latitude is always directed away from the equator, dispelling the long-standing bouncing wave packet model [Loto’aniu et al., 2005]. EMIC waves are enhanced during magnetic storms [Fraser et al., 2010], as anisotropic energetic ring current ions are injected into the inner magnetosphere [Jordanova et al., 2001]. EMIC waves can cause rapid scattering and loss for ring current ions [Jordanova et al., 2001, 2006] and relativistic electrons above 0.5 MeV [Thorne and Kennel, 1971: Lyons and Thorne, 1972; Albert, 2003; Summers and Thorne, 2003; Meredith et al., 2003a]. Favored regions for EMIC excitation include the overlap between the ring current and the plasmasphere [Pickett et al., 2010], dayside drainage plumes [Morley et al., 2009], and the outer dayside magnetosphere in association with solar wind pressure fluctuations [Arnoldy et al, 2005; Usanova et al., 2008; McCollough et al., 2009]. Theoretical global modeling of EMIC wave excitation has confirmed the plasmapause and plume as favored regions of cyclotron resonant instability [Jordanova et al., 2007; Chen et al., 2010a] and demonstrated that the wave excitation can also be enhanced by density fluctuations within a plume [Chen et al., 2009a]. Hybrid codes have recently been used to evaluate the spectral properties and ultimate saturation amplitudes of EMIC waves [Hu and Denton, 2009; Omidi et al., 2010].
Electron Cyclotron Harmonic (ECH) waves are electrostatic emissions, which occur in harmonic bands between multiples of the electron gyrofrequency. These waves are excited by the loss cone instability of injected plasma sheet electrons [e.g., Horne and Thorne, 2000]. The global distribution of ECH emission intensity and its dependence on geomagnetic activity has been analyzed by Meredith et al. [2009b] and shown to be similar to that of chorus. Although ECH emissions contribute to the scattering loss of plasma sheet electrons below a few keV at larger L > 8 [Ni et al., 2012] ECH waves play little role in energetic (> 30 keV) radiation belt dynamics.
The Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) investigation provides the key wave and DC magnetic field observations which, together with the EFW electric field measurements and the RBSP particle measurements, will allow us to identify the origin of all plasma waves important for radiation belt physics, as well as the evolution of the storm-time ring current, and to quantify their influences on the variability of trapped radiation belt particles.